Category: Snippets and Inspiration

For a previous project a generative music system was implemented in Unity featuring rich sounding ensemble strings based on PADSynth. PADsynth is an algorithm designed by Nasca Octavian Paul that generates complex wavetables by varying the width of harmonics in the frequency spectrum, and using the Inverse Fast Fourier Transform (IFFT) to convert it to a time domain audio signal.

The general idea behind the PADSynth algorithm is that complex sounding ensembles are the result of randomized phases and Gaussian distributions in harmonic content. If this sounds a bit abstract you could think of it as this: in an acoustic string ensemble all instruments ever so slightly out-of-tune because of small variations in instrument materials, dimensions, tuning, age, et cetera. There variations become more pronounced in higher frequency content. By widening the bandwidth of higher frequency harmonic content one can create airy pads or choir wavetables.

Below are two clips recorded from the PADSynth implementation in Unity.

The need for an Inverse Fast Fourier Transform (IFFT) comes into play when converting frequency domain content to time domain content. Unity affords an FFT operation which converts time domain audio to a frequency domain spectrum data on an AudioSource through the method GetSpectrumData, however it doesn’t afford a method that does the inverse: convert spectrum data back to a time domain audio signal.

There are some very powerful FFT libraries available such as FFTW (Frigo & Johnson 2003) that afford performance optimized IFFT, however they’re a bit of a hassle to use with a Unity project unless you’re using a C# wrapper such as Szalay’s FFTWSharp (2015). For the purpose of getting intimately familiar with FFT/IFFT and in the spirit of Open Science the choice was made to write a custom C# script.

Inverse Fast Fourier Transform

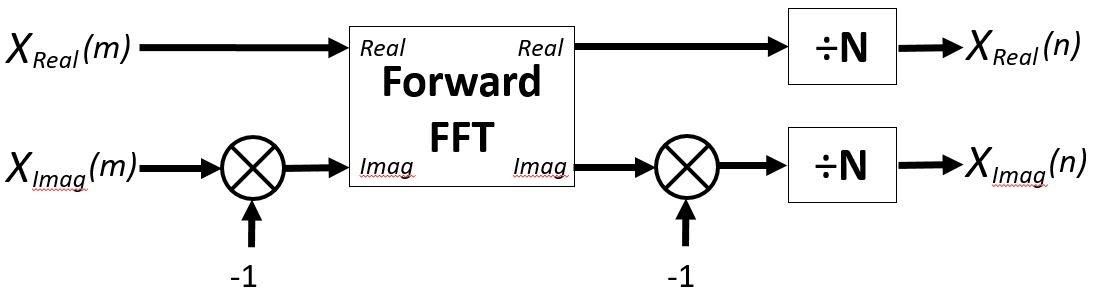
After spending a weekend looking into FFT it turned out IFFT wasn’t nearly as complicated as expected. In fact it’s possible to compute an Inverse FFT by using the Forward FFT algorithm by way of complex conjugation.

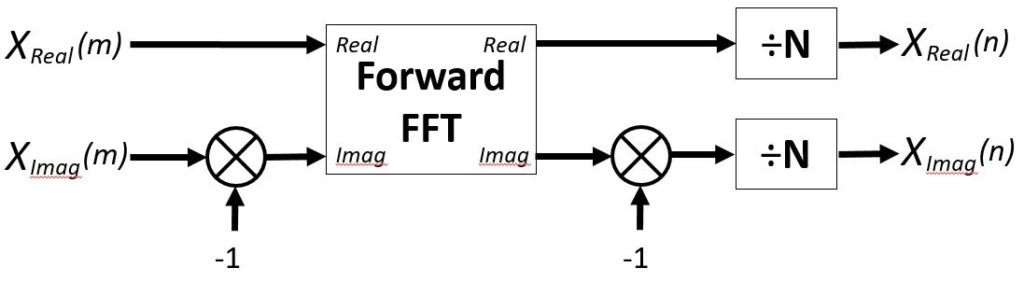
This results in a real-valued time signal so the imaginary part can be discarded, hence in the C# implementation below there’s no second inversion of the imaginary part and only the real part is normalized and returned.

Below you can find the IFFT algorithm implementation used for the PADSynth test in Unity, arrays real and imag are assumed to have the exact same length.

public float[] GetSamplesFromSpectrum(float[] real, float[] imag)
{
	uint windowSize = (uint)real.Length;
	uint n = windowSize;
	uint j = n / 2;
	float temp;	
					
	for (uint i = 1; i < windowSize - 2; i++) 
	{
		imag[i] = -imag[i];
		
		if (i < j)
		{
			temp = real[j];
			real[j] = real[i];
			real[i] = temp;
			
			temp = imag[j];
			imag[j] = imag[i];
			imag[i] = temp;
		}

		uint k = windowSize >> 1;
		while (k <= j)
		{
			j -= k;
			k >>= 1;
		}
		j += k;
	}
		
	uint windowEnd = 1;
	
	uint bitCount = (uint)Mathf.Log(windowSize, 2);
	for (uint lp = 0; lp < bitCount; lp++)
	{
		float re = 1.0f;
		float im = 0.0f;
		
		float c =  Mathf.Cos(Mathf.PI / windowEnd);
		float s = -Mathf.Sin(Mathf.PI / windowEnd);
		float tsr, tsi;

		for (j = 0; j < windowEnd; j++)
		{
			for (uint i = j; i < n; i += windowEnd * 2)
			{
				uint k = i + windowEnd;
				
				tsr = real[k] * re - imag[k] * im;
				tsi = real[k] * im + imag[k] * re;
				
				real[k] = real[i] - tsr;
				imag[k] = imag[i] - tsi;
				real[i] = real[i] + tsr;
				imag[i] = imag[i] + tsi;
			}	
			
			tsr = re;
			re = tsr * c - im * s;
			im = tsr * s + im * c;
		}
		
		windowEnd <<= 1;
	}

	for (uint i = 0; i < n; i++)
	{
		real[i] = real[i] / n;
	}

	return real;
}		

The code wasn’t thoroughly tested but it produced the intended results for the PADSynth implementation. It’s made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. https://creativecommons.org/publicdomain/zero/1.0/.

References
Frigo, M., Johnson, S. (2003). FFTW. Massachusetts Institute of Technology. [Available here]

Lyons, R. (2015). Four Ways to Compute an Inverse FFT Using the Forward FFT Algorithm. DSP Related. [Available here]

Nasca, P. (2011). Padsynth Sound Synthesis Algorithm. Studia Universitatis Babes-Bolyai, Informatica [Available here]

Szalay, T. (2015). FFTWSharp. GitHub. [Available here]