Author: Niels Keetels

Categories
R&D Snippets and Inspiration

DIY Inverse Fast Fourier Transform (IFFT)

For a previous project a generative music system was implemented in Unity featuring rich sounding ensemble strings based on PADSynth. PADsynth is an algorithm designed by Nasca Octavian Paul that generates complex wavetables by varying the width of harmonics in the frequency spectrum, and using the Inverse Fast Fourier Transform (IFFT) to convert it to a time domain audio signal.

The general idea behind the PADSynth algorithm is that complex sounding ensembles are the result of randomized phases and Gaussian distributions in harmonic content. If this sounds a bit abstract you could think of it as this: in an acoustic string ensemble all instruments ever so slightly out-of-tune because of small variations in instrument materials, dimensions, tuning, age, et cetera. There variations become more pronounced in higher frequency content. By widening the bandwidth of higher frequency harmonic content one can create airy pads or choir wavetables.

Below are two clips recorded from the PADSynth implementation in Unity.

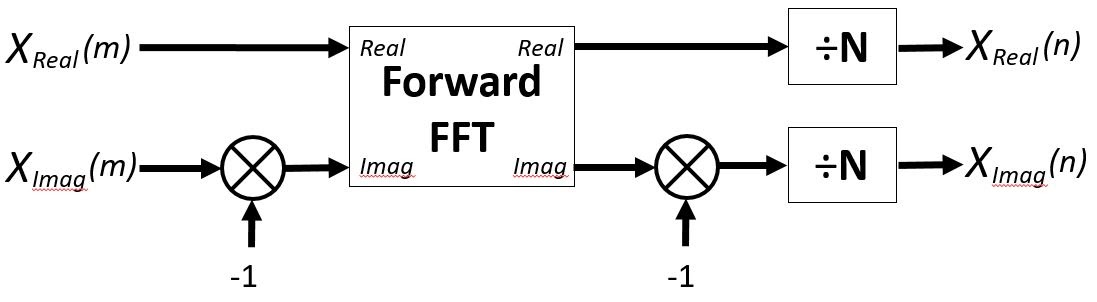
The need for an Inverse Fast Fourier Transform (IFFT) comes into play when converting frequency domain content to time domain content. Unity affords an FFT operation which converts time domain audio to a frequency domain spectrum data on an AudioSource through the method GetSpectrumData, however it doesn’t afford a method that does the inverse: convert spectrum data back to a time domain audio signal.

There are some very powerful FFT libraries available such as FFTW (Frigo & Johnson 2003) that afford performance optimized IFFT, however they’re a bit of a hassle to use with a Unity project unless you’re using a C# wrapper such as Szalay’s FFTWSharp (2015). For the purpose of getting intimately familiar with FFT/IFFT and in the spirit of Open Science the choice was made to write a custom C# script.

Inverse Fast Fourier Transform

After spending a weekend looking into FFT it turned out IFFT wasn’t nearly as complicated as expected. In fact it’s possible to compute an Inverse FFT by using the Forward FFT algorithm by way of complex conjugation.

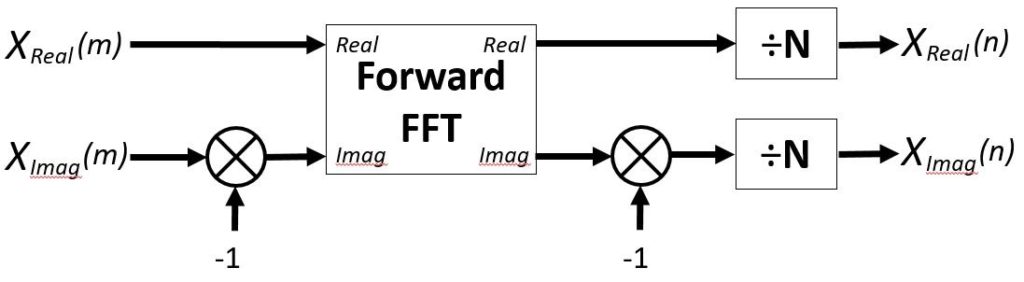
This results in a real-valued time signal so the imaginary part can be discarded, hence in the C# implementation below there’s no second inversion of the imaginary part and only the real part is normalized and returned.

Below you can find the IFFT algorithm implementation used for the PADSynth test in Unity, arrays real and imag are assumed to have the exact same length. 

public float[] GetSamplesFromSpectrum(float[] real, float[] imag)
{
	uint windowSize = (uint)real.Length;
	uint n = windowSize;
	uint j = n / 2;
	float temp;	
					
	for (uint i = 1; i < windowSize - 2; i++) 
	{
		imag[i] = -imag[i];
		
		if (i < j)
		{
			temp = real[j];
			real[j] = real[i];
			real[i] = temp;
			
			temp = imag[j];
			imag[j] = imag[i];
			imag[i] = temp;
		}

		uint k = windowSize >> 1;
		while (k <= j)
		{
			j -= k;
			k >>= 1;
		}
		j += k;
	}
		
	uint windowEnd = 1;
	
	uint bitCount = (uint)Mathf.Log(windowSize, 2);
	for (uint lp = 0; lp < bitCount; lp++)
	{
		float re = 1.0f;
		float im = 0.0f;
		
		float c =  Mathf.Cos(Mathf.PI / windowEnd);
		float s = -Mathf.Sin(Mathf.PI / windowEnd);
		float tsr, tsi;

		for (j = 0; j < windowEnd; j++)
		{
			for (uint i = j; i < n; i += windowEnd * 2)
			{
				uint k = i + windowEnd;
				
				tsr = real[k] * re - imag[k] * im;
				tsi = real[k] * im + imag[k] * re;
				
				real[k] = real[i] - tsr;
				imag[k] = imag[i] - tsi;
				real[i] = real[i] + tsr;
				imag[i] = imag[i] + tsi;
			}	
			
			tsr = re;
			re = tsr * c - im * s;
			im = tsr * s + im * c;
		}
		
		windowEnd <<= 1;
	}

	for (uint i = 0; i < n; i++)
	{
		real[i] = real[i] / n;
	}

	return real;
}

The code wasn’t thoroughly tested but it produced the intended results for the PADSynth implementation. It’s made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. https://creativecommons.org/publicdomain/zero/1.0/.

References
Frigo, M., Johnson, S. (2003). FFTW. Massachusetts Institute of Technology. [Available here]

Lyons, R. (2015). Four Ways to Compute an Inverse FFT Using the Forward FFT Algorithm. DSP Related. [Available here]

Nasca, P. (2011). Padsynth Sound Synthesis Algorithm. Studia Universitatis Babes-Bolyai, Informatica [Available here]

Szalay, T. (2015). FFTWSharp. GitHub. [Available here]

Categories
IRIS Kanaleneiland

Draft assetlist (UI, animations and audio)

Today we created a list of assets that are needed to implement how the user can interact with the player avatar and the environment. Even though the scope of the project is ostensibly very limited, the amount of assets reveals that a lot of work still needs to be done.

Having a huge magnetic whiteboard is invaluable for this sort of activity as the whole team can stand around and provide input. The advantage compared to solutions such as Trello is that it’s easy to see how assets relate to the environment; however, it doesn’t show which assets are currently in development so we decided to also look into embedding Trello in Slack.

Categories
R&D Tutorial

Embedding Unity projects in HTML

In three easy steps you can build, upload and embed your Unity project to be playable online.

Unity used to support a Unity Player plugin for internet browsers, however, using the iframe widget it’s easier than ever to make your game publicly available on the internet without imposing unnecessary hurdles. Follow these three steps to embed your Unity project in HTML based websites.

Step 1: build for WebGL

Open the Build Settings window (File -> Build Settings), select “WebG:” from the list of platforms and if necessary refer to the WebGL project documentation for recommended build settings.

Unity conveniently creates an index.html document for you that loads the game.

Step 2: upload your WebGL build

Upload the build consisting of an index.html document and two folders named “build” and “templateData” to a new folder on a public server. If you are new to FTP Servers, download Filezilla and login to your server to upload files.

For example, we uploaded one of our pilot projects to www.innovatiestudio.hku.nl/LEC_WebGL/

Should you paste the URL in your webbrowser it should already load and run the Unity project as long as WebGL is supported by your browser ( Chrome, Firefox, Internet Explorer, Opera, and Safari are known to have good WebGL support).

Step 3: insert HTML code in your website

To embed the Unity project into your website you need to insert an iframe tag into HTML code, alternatively when using WordPress you can add HTML for text formatting.

Using the iframe-tag you can embed another document inside the document you’re working in, so this way you could just embed the index.html document that Unity generated inside your website. To do this copy the HTML quote below, paste it into your HTML document and change the “src” attribute to the path of your own Unity build.

For example, this is the HTML script used to embed the pilot project into the InnovatieStudio WordPress website:

<iframe src="https://innovatiestudio.hku.nl/LEC_WebGL/index.html" 
    class="webgl-content" style="border:0px #000000 none;" 
    scrolling="no" frameborder="1" marginheight="px" 
    marginwidth="960px" height="600px" width="960px">
</iframe>

To preserve the indended dislay ratio it’s generally a good idea to copy the width and height parameters from the index.hrml document that came with the build.

You can find an example of an embedded Unity Player in our Treetale post.

References:
Arango, Ricardo (2016). How Can I Make The Canvas Transparent On WebGL? Unity. [Available here].

Unity Documentation (2019). Building and running a WebGL project. Unity. [Available here]

Categories
Exploration Nieuws R&D

The Kleinian Group experiment

This isn’t the title of an upcoming Dan Brown novel, it’s an exploration of a fractal type that’s also referred to as the Apollonian limit set.

“A disco for parasites” is a real-time raymarched Kleinian group fractal.

Fractals have long been the domain of mathematicians and computer graphics programmers, however with the recent advances in procedural content generation and real-time image rendering techniques such as raymarching, their recursive and often mesmerising quality would seemingly lend them well for making art and video game content. For this experiment I chose the Apollonian gasket, a limit set of the Kleinian group that in my opinion produces quite natural looking patterns. And here we already stumble upon the first barrier one often encounters when looking into how fractals work: the theory is jargon ridden. With this article I aim to provide an accessible entry point to understanding the Apollonian gasket which afforded me to create “a disco for parasites”.

The fractal-like pattern called the Apollonian gasket used to create “a disco for parasites” is generated by recursively applying Möbius transformations to a set of circles located in some particular positions. The initial configuration of circles is bounded by some sort of shape and must satisfy the condition that they’re externally tangential, in other words their edges touch. Every subsequent iteration fits circles inside the negative space left by the previous iteration.

Source: http://mathworld.wolfram.com/ApollonianGasket.html

The curvature of a circle is equal to the reciprocal of its radius (1 / r) and from this follows that the larger the circle is, the smaller the curvature (a curvature of 0 would look like a straight line). 

float ApollonianGasket(vec3 p)
{
    float scale = 1.0;

    for (int i = 0; i < ITERATIONS; i++)
    {        
        p = 2.0 * clamp(p, -vec3(1.0), vec3(1.0)) - p;

        float sqrRadius = dot(p, p);

        p /= sqrRadius;
        scale /= sqrRadius;
    }

    return 0.2 * abs(p.y) / scale;
}

[Shadertoy] Basic Apollonian gasket that results in the image on the left. Please note that the fractal is mirrored across the X-axis here.

Using a very basic raymarching approach the fractal can be represented in 3D. 

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    vec2 uv = (2.0 * fragCoord - iResolution.xy) / iResolution.y;

    vec3 ro = vec3(0.0,  3.0, -5.0);
    vec3 rd = normalize(vec3(uv, 0.0) - ro);

    float dist = Raymarch(ro, rd);

    vec3 color = vec3(0.0);
    if (dist > 0.0)
    {       
        vec3 N = calcNormal(ro + dist * rd);
        vec3 L = vec3(0,0,-1);

        color = max(vec3(0), dot(N, L));
    }

    fragColor = vec4(color, 1);
}

[Shadertoy] Raymarching + surface normal calculation.

The final representation distorts the fractal to break the symmetries and make it look more organic. I got interesting results by offsetting the radius, in the case of “a disco for parasites”:

float sqrRadius = dot(p, p + sin(p.x * 0.3) + sin(p.z * 0.25) + sin(p.y * 0.14));

This resulted in a distorted 3D Apollonian gasket representation, and by experimentally rotating and offsetting the origin and direction vectors a photogenic view was found.

Texturing and lighting

Texturing proved to be more straightforward than expected. Commonly used strategies for texturing signed distance fields are triplanar mapping and cubemap lookups, however notwithstanding some stretching and mirroring artifacts it turned out that the components of vector p coud just be scaled and used for lookup in tiling 2D diffuse maps for a quite convincing result.

Physically based shading was used for lighting and the red component sampled from the diffuse map using the aforementioned texture coordinates was used for the roughness attribute of the material.

Literature:

Hill, Stephen., et al. (2013). Physically Based Shading in Theory and Practice. SIGGRAPH. [Available here]

Yáñez Escanciano, Jorge. (2017). An introduction to the limit set of Kleinian groups Master Thesis, Universidad Nacional de Educación a Distancia (España). Facultad de Ciencias [Available here]