This isn’t the title of an upcoming Dan Brown novel, it’s an exploration of a fractal type that’s also referred to as the Apollonian limit set.

Fractals have long been the domain of mathematicians and computer graphics programmers, however with the recent advances in procedural content generation and real-time image rendering techniques such as raymarching, their recursive and often mesmerising quality would seemingly lend them well for making art and video game content. For this experiment I chose the Apollonian gasket, a limit set of the Kleinian group that in my opinion produces quite natural looking patterns. And here we already stumble upon the first barrier one often encounters when looking into how fractals work: the theory is jargon ridden. With this article I aim to provide an accessible entry point to understanding the Apollonian gasket which afforded me to create “a disco for parasites”.
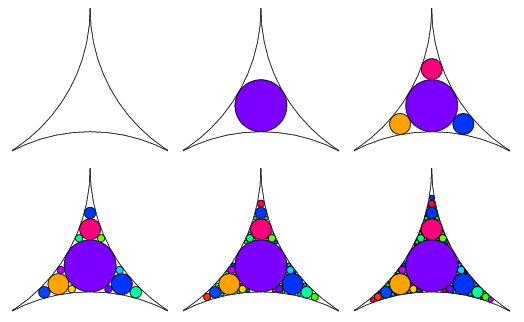
The fractal-like pattern called the Apollonian gasket used to create “a disco for parasites” is generated by recursively applying Möbius transformations to a set of circles located in some particular positions. The initial configuration of circles is bounded by some sort of shape and must satisfy the condition that they’re externally tangential, in other words their edges touch. Every subsequent iteration fits circles inside the negative space left by the previous iteration.
The curvature of a circle is equal to the reciprocal of its radius (1 / r) and from this follows that the larger the circle is, the smaller the curvature (a curvature of 0 would look like a straight line).

float ApollonianGasket(vec3 p) { float scale = 1.0; for (int i = 0; i < ITERATIONS; i++) { p = 2.0 * clamp(p, -vec3(1.0), vec3(1.0)) - p; float sqrRadius = dot(p, p); p /= sqrRadius; scale /= sqrRadius; } return 0.2 * abs(p.y) / scale; }
[Shadertoy] Basic Apollonian gasket that results in the image on the left. Please note that the fractal is mirrored across the X-axis here.
Using a very basic raymarching approach the fractal can be represented in 3D.

void mainImage( out vec4 fragColor, in vec2 fragCoord ) { vec2 uv = (2.0 * fragCoord - iResolution.xy) / iResolution.y; vec3 ro = vec3(0.0, 3.0, -5.0); vec3 rd = normalize(vec3(uv, 0.0) - ro); float dist = Raymarch(ro, rd); vec3 color = vec3(0.0); if (dist > 0.0) { vec3 N = calcNormal(ro + dist * rd); vec3 L = vec3(0,0,-1); color = max(vec3(0), dot(N, L)); } fragColor = vec4(color, 1); }
[Shadertoy] Raymarching + surface normal calculation.
The final representation distorts the fractal to break the symmetries and make it look more organic. I got interesting results by offsetting the radius, in the case of “a disco for parasites”:
float sqrRadius = dot(p, p + sin(p.x * 0.3) + sin(p.z * 0.25) + sin(p.y * 0.14));
This resulted in a distorted 3D Apollonian gasket representation, and by experimentally rotating and offsetting the origin and direction vectors a photogenic view was found.
Texturing and lighting
Texturing proved to be more straightforward than expected. Commonly used strategies for texturing signed distance fields are triplanar mapping and cubemap lookups, however notwithstanding some stretching and mirroring artifacts it turned out that the components of vector p coud just be scaled and used for lookup in tiling 2D diffuse maps for a quite convincing result.
Physically based shading was used for lighting and the red component sampled from the diffuse map using the aforementioned texture coordinates was used for the roughness attribute of the material.
Literature:
Hill, Stephen., et al. (2013). Physically Based Shading in Theory and Practice. SIGGRAPH. [Available here]
Yáñez Escanciano, Jorge. (2017). An introduction to the limit set of Kleinian groups Master Thesis, Universidad Nacional de Educación a Distancia (España). Facultad de Ciencias [Available here]